466C. Number of Ways
You've got array a[1], a[2], ..., a[n], consisting of n integers. Count the number of ways to split all the elements of the array into three contiguous parts so that the sum of elements in each part is the same.
More formally, you need to find the number of such pairs of indices i, j (2 ≤ i ≤ j ≤ n - 1), that (아래식 참고).
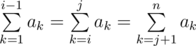
배열을 3등분하는 구간이 몇 개인지 찾는 문제인데, 누적합의 3의 배수로 파악해야 한다는 점에서 약간 애드 혹 알고리즘같은 느낌이 들었다. 누적합을 구해두고 난 후에 총합의 3분의 1 지점이 나오면 cnt1을 하나 증가시키고, 3분의 2 지점이 나오면 지금까지의 cnt1 값을 최종 정답에 더하면 된다. 즉 3분의 1 지점의 개수를 3분의 2 지점마다 업데이트 시켜주는 것이다. 특히 total이 0인 경우를 주의해서 if 문을 작성해주자.
#include <bits/stdc++.h>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
int n; cin >> n;
long long ans = 0, total = 0, total3 = 0, cnt1 = 0;
// Prefix Sum
vector<long long> vec(n), psum(n+1);
for (int i = 0; i < n; i++) cin >> vec[i];
psum[0] = 0;
for (int i = 1; i <= n; i++) psum[i] = psum[i - 1] + vec[i - 1];
// Calculate
total = psum[n];
if (total % 3 != 0) { ans = 0; }
else {
total3 = total / 3;
for (int i = 1; i < n; i++) {
if (psum[i] == total3 * 2) ans += cnt1;
if (psum[i] == total3) cnt1++;
}
}
cout << ans << endl;
return 0;
}'학부 수업 정리 > 알고리즘연습 (22-1)' 카테고리의 다른 글
| [알고연] (3주차-1) 734B. Anton and Digits (0) | 2022.03.17 |
|---|---|
| [알고연] (2주차-3) 1285B. Just Eat It! (0) | 2022.03.10 |
| [알고연] (2주차-1) 1003C. Intense Heat (0) | 2022.03.10 |
| [알고연] (1주차-3) 118A. String Task (0) | 2022.03.05 |
| [알고연] (1주차-2) 71A. Way Too Long Words (0) | 2022.03.05 |