1. Minimum Spanning Tree (MST)
Spanning Tree는 그래프의 모든 정점과 간선의 부분집합으로 구성된 부분 그래프이다. MST는 주어진 그래프의 연결 그래프들 중 엣지들의 비용이 최소가 되도록 하는 그래프를 의미한다. (단, 사이클을 생성하지 않아야 한다.)
2. Prim 알고리즘의 Idea
- 아무 노드 중 하나의 노드를 가진 트리에서 시작
- 트리에 인접한 edge들 중에서 가장 작은 weight를 가진 edge를 추가 (단, 사이클을 만들지 않아야 함)
- Spanning Tree가 될때까지 이 과정을 반복 (최종적으로 node $n$개 - edge $n-1$개가 되어야 함
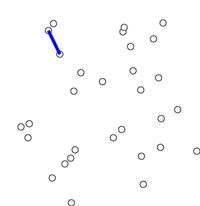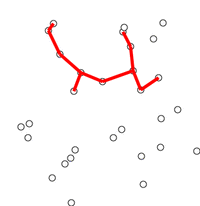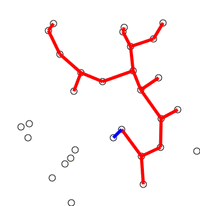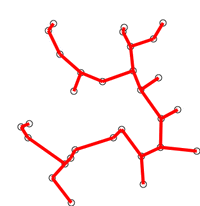
3. Prim 알고리즘의 정당성 증명
- 입력 그래프: $G = (V, E)$
- Edge Set인 $T_{mst}$ 는 정답 중 하나라고 가정
- 알고리즘이 끝난 후 Prim 알고리즘이 가지고 있는 edge set $T$는 $T_{mst}$가 될 것이다.
※ 주의사항: $T_{mst}$는 증명 중간에 바뀔 수 있기 때문에 미리 잡고 시작할 수 없다. 하지만 정답이라는 사실은 항상 유지된다!
$\exists\ T_{mst} \rightarrow T \subseteq T_{mst}$ : Prim Algorithm이 가지고 있는 edge set $T$는 어떤 정답의 부분집합임을 증명하자.
- Base: 알고리즘 시작 시 node 1개, edge 0개이므로 $T = \varnothing$ 이다. 따라서, $T \subseteq T_{mst}$ 가 항상 성립한다.
- Step: 어떤 시점에 $T \subseteq T_{mst}$ 라고 가정하자. 이후 한 스텝을 진행해서 Prim Algorithm이 edge $e_1$ 을 추가하고 현재 edge set 은 $T' = T \cup \left\{ e_1 \right\}$ 이다.
- Case 1: $T' \subseteq T_{mst}$ 이면 명제 성립하고 끝!
- Case 2: $T' \nsubseteq T_{mst}$ 이면 반드시 사이클이 생성된다. 이 경우 사이클 내부에 $(e \neq e_1) \ \land (e \notin T') \ \land (T \cup \left\{ e \right\} \text{is not a cycle}) \ \land (e\text{ is connected to } T)$ 를 만족하는 edge $e$가 반드시 존재한다.
위의 Case 2 에서 $W(e_1)$ 과 $W(e)$ 의 대소관계에 따른 케이스를 나눠서 생각해보자.
- Case 2-1: $W(e_1) > W(e)$ 이면 알고리즘은 항상 작은 것만 넣어야 하는데 더 작은 것이 존재한다는 뜻이므로 알고리즘에 모순된다.
- Case 2-2: $W(e_1) < W(e)$ 이면 $(T_{mst} - \left\{ e \right\}) \cup \left\{ e_1 \right\}$ 인 더 좋은 답이 존재하게 되므로 $T_{mst}$의 정의에 모순된다.
- Case 2-3: $W(e_1) = W(e)$ 이면 $(T_{mst} - \left\{ e \right\}) \cup \left\{ e_1 \right\}$ 이것도 정답이 된다. 이 집합을 $T'_{mst}$ 라고 하면 $T' \subseteq T'_{mst}$ 이므로 명제가 성립한다. 증명 끝!!
4. Prim 알고리즘의 구현과 성능
정점 개수 n, 엣지 개수 m이라고 하자.
- Graph 표현: Linked List 로 구현. 각 노드에는 연결된 엣지들이 $(goal node, weight)$ 형태로 저장되어 있다. (사용 시간: $m$)
- 노드가 트리에 들어갔는지 마킹: 노드 길이만큼 일반 배열 생성해서 구현. boolean 값으로 몇번 노드가 있는지 없는지만 확인하는 용도이다. 중복과 사이클 여부를 판별할 때도 사용 가능하다. (사용 시간: edge 하나 꺼낼때마다 2칸씩 확인하므로 총 $4n$)
- Edge 저장소: Priority Queue로 구현. 노드에 연결된 엣지들은 $(node1, node2, weight)$ 형태로 저장한다. (사용 시간: 모든 edge들이 2번씩 넣고 빠지고, 우선순위 큐를 사용하므로 총 $2m\log n$)
- 시간복잡도: $O(m\log n)$
'학부 수업 정리 > 알고리즘 (21-2)' 카테고리의 다른 글
| [알고리즘] 6. Tape Storage (0) | 2021.12.27 |
|---|---|
| [알고리즘] 5. Deadline Scheduling (0) | 2021.12.27 |
| [알고리즘] 4. 최단 거리 - Dijkstra 알고리즘 (0) | 2021.12.27 |
| [알고리즘] 3. MST - Kruskal 알고리즘 (0) | 2021.12.27 |
| [알고리즘] 1. 수학적 귀납법과 재귀 (0) | 2021.12.27 |

